Let A, B,C be square matrices such that AC = CB and C is invertible. If A is an eigenvalue of A, sh…

Let A,B and C be square matrices such that AB=AC , If A \neq 0 , then B=C ... | PlainmathПодробнее

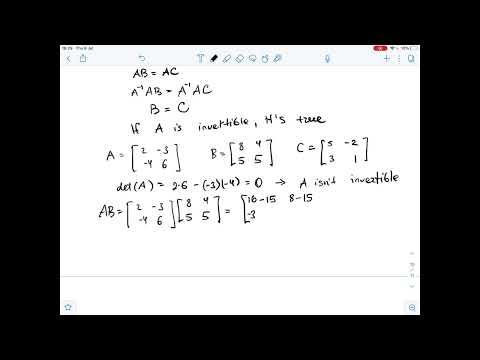
$Let A,B and C be square matrices such that AB=AC , If A \neq 0 , then B=C ... | Plainmath$

If the product D=ABC of three square matrices is invertible , then A must be ... | PlainmathПодробнее

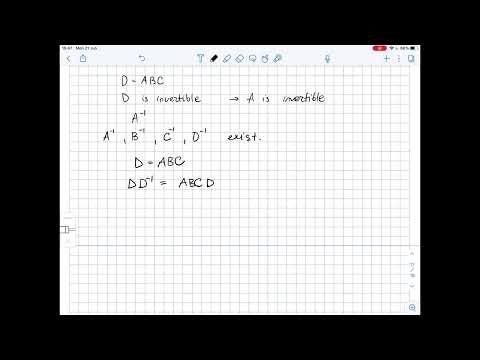
Let where B and C are square matrices. (a) If Î» is an eigenvalue of B with eigenvector x = (x1,...…Подробнее

Let $ A, B, C $ be three square matrices such that $ A B C+A B+ $ $ B C+A C+A+B+C=O $. If ...Подробнее

$Let $ A, B, C $ be three square matrices such that $ A B C+A B+ $ $ B C+A C+A+B+C=O $. If ...$

Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebraПодробнее

Let $A, B, C$ be three square matrices such that $A B C+A B$ $+B C+A C+A+B+C=O$. If $A$ ....Подробнее

$Let $A, B, C$ be three square matrices such that $A B C+A B$ $+B C+A C+A+B+C=O$. If $A$ ....$

If A, B and C are the square matrices of the same order and AB implies B = C, then A. A is sing...Подробнее

Lecture#129:Theorem A square Matrix A is invertible Iff each Eigen Value of A is non-zeroПодробнее

Let B=[1 3 1 5] and A be a 2*2 Matrix such that AB^-1=A^-1. If BCB^-1=A and C^4+aC^2+BI=0, then 2B-aПодробнее

Prove that the Product of Invertible Matrices is Invertible and (AB)^(-1) = B^(-1)A^(-1)Подробнее

A is Invertible and AB = AC Prove B = C If A is Singular find 2 Matrices where AB =AC P 2-5-6Подробнее

Adjoint of 2×2 MatrixПодробнее

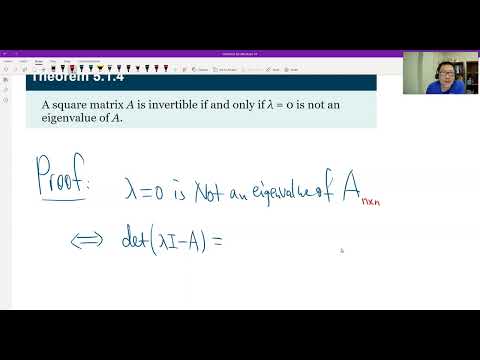
Theorem 5.1.4 (Eigenvalue and Invertibility)Подробнее

Let `A, B, C` be square matrices of the same order `n`. If `A` is a non singular matrix, then if `ABПодробнее

non invertible matrix . find c so that matrix A-CI2 is non invertible #matrixalgebra #dsu #lse #mitПодробнее

MATH 3191: Eigenvalues and The Invertible Matrix TheoremПодробнее

Subtraction of Matrices Class 9Подробнее

Актуальное