Let `A, B, C` be square matrices of the same order `n`. If `A` is a non singular matrix, then if `AB

If A, B are non singular square matrices of same order, then adj(AB) = (adjB)(adjA) | 11 | MATRI...Подробнее

MSBTE | M1 Backlog | Basic Mathematics 22103 | MCQ on Matrices...Подробнее

Let `A, B, C` be square matrices of the same order `n`. If `A` is a non singular matrix, thenПодробнее

If B is a non-singular matrix and A is a square matrix then det(B −1 AB) linear algebraПодробнее

If A,B are non-singular square matrices of same order; then `adj(AB) = (adjB)(adjA)`Подробнее
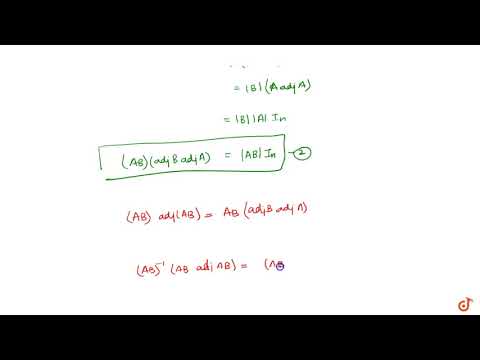
If A, B and C are the square matrices of the same order and AB implies B = C, then A. A is sing...Подробнее

Prove that the Product of Invertible Matrices is Invertible and (AB)^(-1) = B^(-1)A^(-1)Подробнее

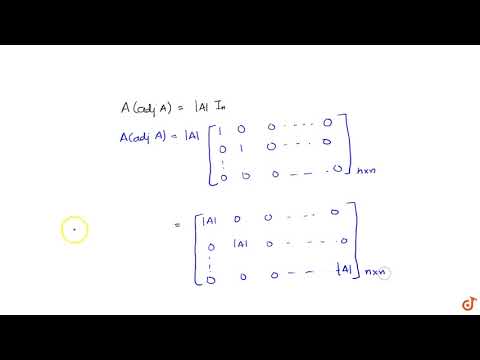
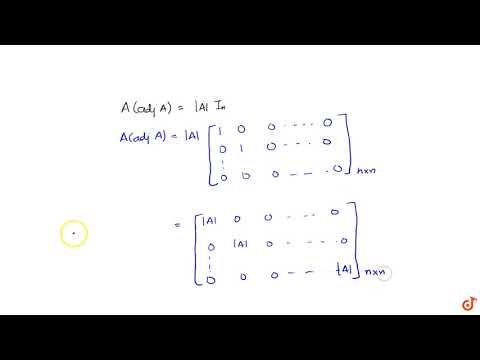
Let A be a non-singular square matrix of order n. Then; `|adjA| = |A|^(n-1)`Подробнее
If A and B are nonsingular matrices of same order, then AB and BA are also nonsingular matrices of..Подробнее

If |■(a-b-c&2a&2a@2b&b-c-a&2b@2c&2c&c-a-b)|= (a+b+c) (x+a+b+c)Подробнее

Determinant of a Matrix Class 9Подробнее

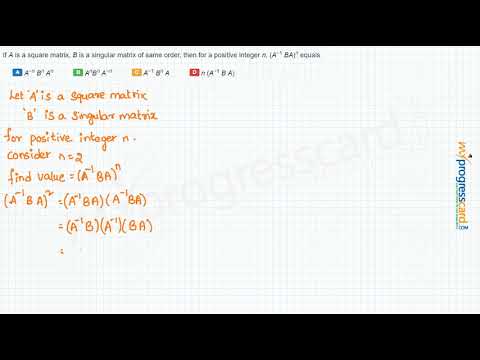
If A is a square matrix, B is a singular matrix of same orderПодробнее
If A, B are non singular square matrices of the same order then (AB-¹)-¹= | Class 10 Math sampleПодробнее

Let A be a nonsingular square matrix of order 3×3 . Then determinant adjoin A is equal toПодробнее

Class 12th – Prove (AB) Inverse = B Inverse A Inverse | Matrices | Tutorials PointПодробнее

Non-Singular Matrices Are INVERTIBLE | FREE Linear Algebra CourseПодробнее

If \( A \) is a non-singular square matrix of order \( n \), then the rank of \( A \) is (A) equ...Подробнее

If B is a non-singular matrix and A is a square matrix, then det (B^-1 AB) is equal toПодробнее

Let A be a non-singular square matrix of order n. Then; `|adjA| = |A|^(n-1)`Подробнее
Inverse of Matrices - Theorem#3 | If A and B be two non-singular Matrices of the same order, n thenПодробнее
