Last 2 digits using Euler's Totient Function
Find the last two digits of 3^431 without using a^φ(n)==1 (mod n) Totient functionПодробнее

Number Theory | Euler's Theorem | The last two digits of a numberПодробнее

4. Eulers Theorem | Last digit | Last 2 digit || Phi of a numberПодробнее

Calculate the Last 2 Digits of a Tower of Powers in Number TheoryПодробнее

Last 2 digits using Euler's Totient FunctionПодробнее

Last 2 digits of 89^122 - 3 methods with Binomial Theorem, Euler's Theorem, and Modular PowersПодробнее

The last two digits of a number | application of Fermat-Euler's theoremПодробнее

521 math #127: The last two digits (Euler's Totient Function?)Подробнее

Euler’s Totient Function (Solved Examples)Подробнее
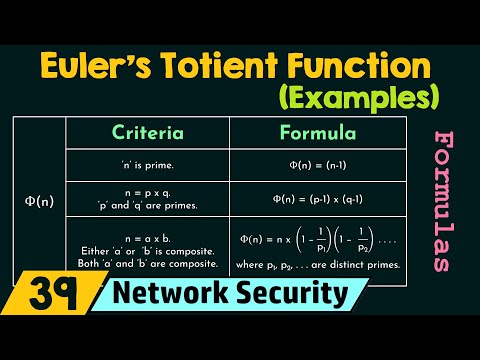
Euler’s Totient Function (Phi Function)Подробнее

Найти последние цифры числа 2¹⁰⁰⁰ ... и даже больше!Подробнее

Find the last two digits.Подробнее

Eulers theorem to find remainders |number system tricks for CATПодробнее

Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximationsПодробнее
Euler's phi function |Solved examples |CryptographyПодробнее

Intro to Chinese Remainder Theorem and Euler's Totient Theorem via a Challenging ProblemПодробнее

Last digit or last two digit of a number using Euler theorem | Number SystemПодробнее
