✨ If A and B are non singular matrix, then prove that (AB)^-1=B^-1.A^-1.✨✨🤔🤔🤔🤔🤔🤔

1.If A and B are symmetric matrices, prove that AB − BA is a skew symmetric matrix.Подробнее

AB and BA matrix multiplication solving simple wayПодробнее

If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrixПодробнее

If A, B are non singular square matrices of same order, then adj(AB) = (adjB)(adjA) | 11 | MATRI...Подробнее

If A and B are invertible matrices of the same order, then (AB)^(-1) is equal to : | CLASS 12 |...Подробнее

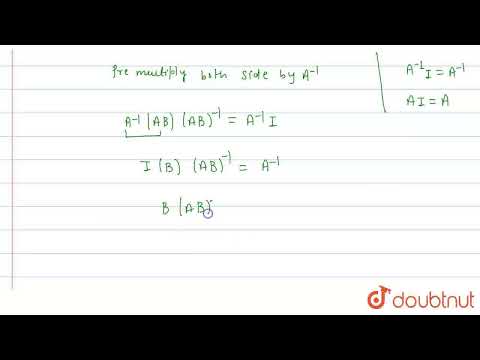
If A is non-singular matrix then prove that A౼¹ =AdjA/detAПодробнее

If A and B are invertible square matrices of the same order then (A B)^-1= ? (a) A B^-1 (b) A^-1 ...Подробнее

If A is a non-singular matrix then prove that `A^(-1) = (adjA)/(|A|)`. | Class 12 Maths | DoubtnutПодробнее

If A & B are non-singular matrices of the same order then Prove that AB & BA are also non-singular..Подробнее

Prove that the Product of Invertible Matrices is Invertible and (AB)^(-1) = B^(-1)A^(-1)Подробнее

Define inverse of a matrix and prove that (AB)-1=B-1.A-1Подробнее

Proof of (AB) -1 = B-1A-1 // mathematics class 9 // topic 6Подробнее

DEFINE INVERTIBLE MATRICES || PROVE THAT (AB)^-1 = B^-1A^-1 || P T(ab)^-1= b^-1a^-1Подробнее

Inverse of Matrices - Theorem#3 | If A and B be two non-singular Matrices of the same order, n thenПодробнее

If `A` and `B` are symmetric non singular matrices, `AB=BA` and `A^(-1) B^(-1)` exists then proveПодробнее

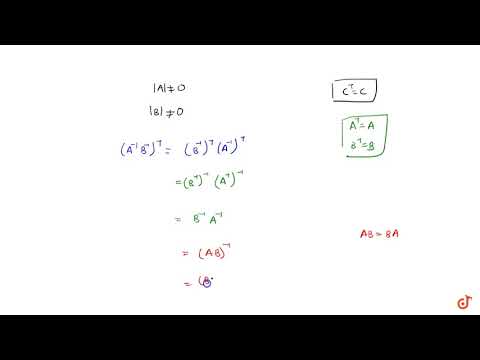
If A; B are invertible matrices of the same order; then show that `(AB)^-1 = B^-1 A^-1`Подробнее

If `A and B` be two non singular matrices and `A^-1 and B^-1` are their respective inverse, thПодробнее

Class 12th – Prove (AB) Inverse = B Inverse A Inverse | Matrices | Tutorials PointПодробнее